Peter Edwards has just given the 2015 Hofmann lecture here at Imperial on the topic of solvated electrons. An organic chemist knows this species as “e–” and it occurs in ionic compounds known as electrides; chloride = the negative anion of a chlorine atom, hence electride = the negative anion of an electron. It struck me how very odd these molecules are and so I thought I might share here some properties I computed after the lecture for a specific electride known as GAVKIS.[1] If you really want to learn (almost) everything about these strange species, go read the wonderful review by Zurek, Edwards and Hoffmann,[2] including a lesson in the history of chemistry stretching back almost 200 years.
GAVKIS consists of a tricyclic aza-ether ligand or cryptand wrapping a potassium atom in the centre, the overall unit having no charge. The oxygen and nitrogen heteroatoms coordinate to the metal, in the process evicting its single electron. The question that struck me is “where does that electron go?”. You see in all normal molecules that electrons are associated with either one, two (or rarely) three nuclei, to form one-centred monosynaptic basins (lone pairs), two-centre or disynaptic basins (i.e. bonds) and more rarely three-centre bonds. The shared-electron two-centre manifestation was of course famously introduced by Gilbert N. Lewis in 1916 (note the centenary coming up!). Knowing where the electron (pairs) are has enabled the technique popular with organic chemists known as arrow pushing, or the VSEPR analysis of inorganic compounds. But an electride has no nucleus associated with it! So how can one describe its location?
[jsmol caption=’The crystal structure of GAVFIS’ fileurl=’https://www.rzepa.net/blog/wp-content/uploads/2015/07/GAVFIS-lattice.mol2′ id=’a2′ commands=’=spacefill 23%;wireframe 0.15;color cpk;’ debug=’false’]
The crystal structure of GAVFIS shows the potassium to be 8-coordinate. Remember, x-rays are diffracted not by a nucleus but by electrons in the molecule. The highest densities are of course associated with electrons in inner shells centered on nuclei and the much lower densities found in conventional bonds are not normally located by this technique (but see here). So it is no surprise to find that this x-ray analysis[1] did not succeed in answering the question posed above; where is the single electron liberated from the potassium atom? They did look for it, but surmised only that would be found in the “noise level electron density in the spaces between them (molecules)“. For GAVFIS, that empty space is actually dumb-bell shaped, and so perhaps an answer is that the electron occupies the dumb-bell shaped spaces between the ligand-potassium complex.
X-ray analysis was defeated by noise; it is an experimental technique after all. But the noise in a quantum mechanical calculation is much smaller; can this reveal where the evicted electron is? Here is the spin density (unpaired electron) distribution for one molecule of GAVFIS computed using the UωB97XD/6-31++(G) DFT method.[3] It is a stratocumulus-like cloud that enshrouds the molecule (click on the diagram below and you can rotate the function to view it from your own point of interest) but interestingly avoiding the regions along the N….N axis. There are also tiny amounts of (negative) spin density on the ligand atoms. So even when the “empty space” is infinitely large, the shape of the electride anion is nevertheless quite specific, but a holistic function of the shape of the entire molecule rather than its component atoms.‡
[jsmol caption=’The spin density in GAVFIS’ fileurl=’https://www.rzepa.net/blog/wp-content/uploads/2015/07/GAVFIS_sden.cub.xyz’ id=’a3′ commands=’=isosurface wp-content/uploads/2015/07/GAVFIS_sden.cub.jvxl translucent;zoom 70;’ debug=’false’]
Another way of describing where electrons are is using functions known as molecular orbitals. Below is the SOMO (singly occupied MO) and its shape in this case coincides with that of the spin density.
[jsmol caption=’The SOMO for GAVFIS’ fileurl=’https://www.rzepa.net/blog/wp-content/uploads/2015/07/GAVFIS_gp_mo113.cub.xyz’ id=’a3′ commands=’=isosurface wp-content/uploads/2015/07/GAVFIS_gp_mo113.cub.jvxl translucent;zoom 70;’ debug=’false’]
The molecular electrostatic potential is rather wackier (red = attractive to protons).
[jsmol caption=’The molecular electrostatic potential in GAVFIS’ fileurl=’https://www.rzepa.net/blog/wp-content/uploads/2015/07/GAVFIS_gp_esp.cub.xyz’ id=’a4′ commands=’=isosurface wp-content/uploads/2015/07/GAVFIS_gp_esp.cub.jvxl translucent;zoom 40;’ debug=’false’]
Odder still is the ELF (electron localisation function) and the identification of the centroids of its basins. These centroids normally coincide with the two-centre basins (bonds) and one-centre basins (lone pairs, inner shell electrons) in normal molecules, both being close to nuclear centres (atoms). For GAVFIS, two unexpected one-centre basins are found close to the two nitrogen atoms in the molecule, each with a population of 0.48 electrons, along with regular one-centre “lone pair” basins pointing inwards to the potassium (2.38 electrons each). The odd-looking pair of locations identified for the electride anion may have little physical reality, except for reminding us that the electride can indeed be in more than one location simultaneously!
[jsmol caption=’The ELF centroids in GAVFIS’ fileurl=’https://www.rzepa.net/blog/wp-content/uploads/2015/07/GAVFIS_bas.mol’ id=’a5′ debug=’false’]
I often also use the NCI (non-covalent-interaction) property of the electron density in these blogs. It tells us about regions of non-covalent electron density which represent attractive weak interactions between or within molecules. Here, it again shows us the weak non-covalent density (as the reduced density gradients) wrapping the molecule (green=weakly stabilizing).
[jsmol caption=’The NCI function in GAVFIS’ fileurl=’https://www.rzepa.net/blog/wp-content/uploads/2015/07/GAVFIS-gp-lr.xyz’ id=’a6′ commands=’=isosurface wp-content/uploads/2015/07/GAVFIS-gp-lr.jvxl translucent;zoom 70;’ debug=’false’]
The obvious next question is that if each molecule is surrounded by weak spin density arising from an unpaired electron, would two such species form a dimer in which the spins are paired in an manner analogous to the conventional single bond? The overlap is not going to be fantastic if the spin distribution has the shape shown above, but what the hell. Here is the HOMO of such a species.[4] It appears the shape of the electride is very pliable indeed; they have been squeezed out of the contact region between the two molecules (which form a close contact pair) into wrapping the dimer rather than the monomer! The spin-coupled singlet by the way is about 4.6 kcal/mol more stable in free energy ΔG298 than two isolated monomer doublets, and 5.5 kcal/mol lower than the triplet species[5] which retains two unpaired electrons. A sort of weak molecule-pair bond rather than an atom-pair bond.
[jsmol caption=’The MO in GAVFIS dimer’ fileurl=’https://www.rzepa.net/blog/wp-content/uploads/2015/07/GAVFIS_mo225.cub.xyz’ id=’a8′ commands=’=isosurface wp-content/uploads/2015/07/GAVFIS_mo225.cub.jvxl translucent;zoom 70;’ debug=’false’]
This has hardly started to scratch the surface of the strange properties of electrides. If your appetite has been whetted, go read the article I noted at the beginning.[2]
‡ For normal molecules, a Mulliken or other population analysis reduces the charge and spin density down to an atom-centered distribution. If this is done for GAVFIS, the spin density collapses down to the molecular centroid, in this case the potassium (spin density 1.15). This of course is horribly misleading, and serves to remind us that such atom-centered distributions can sometimes be far from realistic.
References
- D.L. Ward, R.H. Huang, and J.L. Dye, "Structures of alkalides and electrides. I. Structure of potassium cryptand[2.2.2] electride", Acta Crystallographica Section C Crystal Structure Communications, vol. 44, pp. 1374-1376, 1988. https://doi.org/10.1107/s0108270188002847
- E. Zurek, P. Edwards, and R. Hoffmann, "A Molecular Perspective on Lithium–Ammonia Solutions", Angewandte Chemie International Edition, vol. 48, pp. 8198-8232, 2009. https://doi.org/10.1002/anie.200900373
- H.S. Rzepa, "C 18 H 36 K 1 N 2 O 6", 2015. https://doi.org/10.14469/ch/191347
- H.S. Rzepa, "C 36 H 72 K 2 N 4 O 12", 2015. https://doi.org/10.14469/ch/191348
- H.S. Rzepa, "C 36 H 72 K 2 N 4 O 12", 2015. https://doi.org/10.14469/ch/191350
Tags: Interesting chemistry
There have been a couple of tweets asking why I am still using Java to display surfaces.
1. The alternative, JSmol is still rather slow at displaying JVXL surfaces. It is possible if one uses low resolution surfaces, but medium and high res is not really viable.
2. I did try some time ago to get the JSmol WordPress extension working on this instance of the blog. Despite revisiting several times, it still does not work. I suspect only a complete reinstall of the WordPress software and rebuilding from scratch would solve this issue.
3. The syntax used for WP-JSMol is quite different from that used to invoke Java directly on this blog. So I would have to edit the syntax for >200 posts if I were to replace Java by JSmol.
These issues combine to make the migration quite difficult. I have just updated the official Java Jmol applet to the latest release, using the official signed version. It seems to be working.
As an experiment, I have cloned the above post as http://www.rzepa.net/blog/?p=14272
This version uses JSmol to view the interactive objects, and unlike the post here, it works (at least for me). I have been baffled by why it works on the other version but not here for more than a year, and have not yet found the cause. It appears to be some sort of conflict with the other extensions I have installed here, but which one eludes me. Go try the other version, but it might be slow to load.
A nice example of electrides. I used your wavefunction for QTAIM analysis (for the moment just topological analysis) to see where is the electron. It has been suggested that non-nuclear attractors of AIM theory coincide with free electrons. For instance please see:

http://pubs.rsc.org/En/content/articlelanding/2015/cc/c5cc00215j#!divAbstract (doi: 10.1039/C5CC00215J)
or an older paper:
http://www.sciencedirect.com/science/article/pii/S0166128009000931 (doi: 10.1016/j.theochem.2009.02.003)
So, I was curious to see which picture is consistent with AIM picture. You may see the molecular graph here:
https://www.academia.edu/13810211/GAVFIS
AIM picture is in line with the picture obtained from MESP, showing three basins for the free electron.
It is quite different from ELF. I can provide some more information about delocalization of the electronic basins to see which atom is interacting more with them or how localized they are in their positions.
Very nice Cina! Yes, do provide more information. Also, I have edited in your QTAIM analysis into your comment above. And I would add that your topological analysis also matches the NCI function.
For completeness, the doi for the wfn (wavefunction) file I used for the ELF, and which can also be used for QTAIM can be found here: 10.14469/ch/191354
And finally a comment on non-nuclear attractors. My favourite “NNA” is in the H3+ cation, with an NNA at its centre. So its not restricted to free electrons! F2 is another!
You are absolutely right in case of H3+ and the fact that NNAs are not restricted to free electrons. There are more examples of molecules having NNA but no free electron. I had looked at three of them in this old paper in early years of my PhD.
http://www.sciencedirect.com/science/article/pii/S0166128009000931
Interestingly, I noticed that NNAs behave differently! For instance NNAs in the center of H3+ and B3- are delocalized and interact with atoms. I would say they are floppy. It seems to me they are a manifestation of highly delocalized but shared electrons, which promote covalency in the systems that they are associated with.
On the other hand, the NNA in the center of Li3+ is essentially different. Electrons are localized in the center. It reminds me of a definition of metalic bonding I learned in high school. A sea of free electrons loosely bonded to positive atoms. The NNA in the Li3+ interacts with three Li+ atoms as if it is an ionic system with free electrons as anions. I have not seen a detailed analysis of NNA-bonding as in my paper!
P.S. I will send a full AIM analysis of this system once it was completed.
I have obtained the QTAIM analysis of the singlet weak dimer of GAVKIS, but no NNAs are detected (the Poincare-Hopf theorem is satisfied).
I checked it with AIM2000 last night. Now, I am analyzing the wavefunction by AIMAll of Todd Keith. I am curious to see if it can find NNAs or not. AIM2000 is a very powerful tool for topological analysis. Would you please let me know which software you employed for AIM analysis.
I used AIMALL (latest version). It takes a few hours to hunt everything down to the satisfaction of Poincare-Hopf, it tends to be more thorough than AIM2000.
The archive for the singlet dimer can be found at 10.14469/ch/191360.
You are right. AIMAll does not recognize NNAs. My computations finished with no NNA few minutes ago.
However, if you completely remove NNAs still Poincare-Hopf satisfies since the set of critical points that are associated with the NNA are all very flat. So, if AIMAll cannot find NNA, it certainly cannot find other CPs connecting the NNA to the other attractors. I will add NNAs manually into the wavefunction and repeat the analysis by AIMAll to see what I can get.
AIMAll is fast for integration of basin properties but unfortunately is not as precise as AIM2000 for topological analysis. Besides, it is too much user-friendly! It is almost impossible to manipulate it. This case seems to be more interesting than it appeared at first glance.
AIMALL does detect NNAs, but it requires two passes of the program. The first detects the NNAs and writes out a block of data that has to be edited into the .wfn file manually. This is then used to re-run the AIMALL analysis, which will now include them in the paths. I used to use AIM2000, but found it very often missed key points and that the Poincare-Hopf criterion was NOT satisfied. AIMALL has never yet failed me in satisfying this condition.
Yes, I am aware of the process of handling NNAs in AIMAll and a big fan of the software and the developer, Todd. However, It sometimes dismisses slight curvatures and does it for a good reason. Small curvatures might appear in electron density not because of the presence of a real critical point, but due to some flaws in the wavefunction. Poincare-Hopf condition is a good indicator of accuracy of AIM analysis but if a whole set of critical points are missing then Poincare-Hopf condition is not helpful. In this particular case electron density of the NNA and the whole set of CPs associated with is too small. I afraid AIMAll threshold does not recognize the NNA and other low-density CPs in this molecule unless I force the program to look for an NNA. If I could find something, I will return to you.
I agree that if the density topology is very flat, you might find critical points that are quite close. In these circumstances, pairs can annihilate and vanish, and such annihilation of course will also satisfy Poincare-Hopf.
If the density cut-offs in AIMALL are not capturing the weak electride density, this is good to know. So if you can see them for the dimer as well as the monomer, that would be fascinating.
I inserted the NNAs obtained from AIM2000 in the wavefunction and analyzed the system with AIMAll once more. The results are identical to the first analysis; no NNA is identified. However, I noticed something unusual in the SUM file, the output of AIMAll. Please kindly let me know if the result of your analysis is the same.
I see relatively large errors in the total charge (0.2334 au) and total energy of the system. In fact, the energy difference between DFT and AIM (K_Scaled energy) is 0.011463 au (~7.2 kcal/mol). This energy error is too high for integration and confirms that something is missing. I think the density of CPs associated with the NNA is lower than the AIMAll cutoff.
Indeed, accuracy of the energy and charge obtained from an AIM computation is a very important criterion that must be checked to validate results. Even more important than the satisfication of Poincare-Hopf rule. As you can see here the Poincare-Hopf rule is satisfied but the big error confirms that something is remained unidentified by AIMAll.
Observe also for the MEP calculation, it is quite obvious that the standard cube of points from which the isosurface is produced is clearly truncated. This confirms what you write in the previous comment.
I have sent a message to Todd, and it will be interesting to see what he says.
🙂 I did the same! He will receive two emails at a time. He is very open and is developing the program very fast. I hope he adds an option for manipulating cutoffs.
Yet another localisation scheme, the NBO or natural bond orbital method, which strives to recover Lewis-like partitioning of electron pairs or lone pairs. In this instance, it recovers what we already see above in the MO (a fully delocalised form). The electride NBO cannot be localised further.
How would the two of you rate MultiWFN versus AIMAll and AIM2000 for QTAIM topology, basin and attractor analysis?
Unfortunately I have no experience with MultiWFN. I started using AIMAll mostly for its capability for providing magnetic response properties and current density.
http://pubs.acs.org/doi/abs/10.1021/jp202901f
http://pubs.acs.org/doi/abs/10.1021/ct4007184
http://link.springer.com/article/10.1007/s00214-015-1617-7#page-1
Then I got used to the program. I heard positive points about MulitWFN but it would be good to see if it can recover NNAs in this case. And in other cases how accurate and fast it is in computing integration properties?
Brain, are you a MultiWFN user? Can you analyze this system?
There is a considerable literature on electrides, but one recent article is worth including here: doi: 10.1021/jacs.5b00242 together with an earlier review: doi: 10.1021/ar4002922 There the term interstitial quasiatoms (ISQs) is used. I rather fancy these might be the equivalent of the non-nuclear attractors in QTAIM theory?
In an earlier post on the Birch reduction of methoxybenzene using sodium in ammonia (with three ammonias solvating one sodium) I had noted two valence bond or electronic isomers of the system, one with spin density on the sodium and one with spin density on the anisole, separated by about 11 kcal/mol in free energy with the latter the more stable.
No doubt two such electronic states are also possible with electrides, and their relative stability will certainly be a function of the character and number of ligands, and of course the metal.
The paper by Hoffmann reminds me of this old paper by Victor Luana et. al. on the presence of NNA in alkali metal crystals under high pressure. It seems that the authors of the new paper were not aware of this older contribution.
http://scitation.aip.org/content/aip/journal/jcp/119/12/10.1063/1.1600433
It is often the case that different communities come across the same phenomenon, and name them differently. I only realised recently for example that the term chemists use in NMR spectra, “chemical shifts” is named entirely differently by the physics community that also analyses such spectra!
Three years ago, I posted here a blog on Birch reduction of anisole. There I described a pre-complex of Na.3NH3 with anisole where I noted a Mulliken analysis as placing the spin density on the Na, but that another lower energy complex could be located where the spin density transferred to the anisole. I had not then picked up on the observation that a Mulliken analysis of electrides does indeed put the spin density on the metal, but that such an atom-centered decomposition might be quite misleading. I have now added a comment to that post clearly identifying the “pre-complex” as in fact a sodium electride.
Its not just new authors that fail to pick up on old pre-existing results in the literature, its also blog authors who fail to pick up on their own older posts!
Whilst I am on the topic of what might be out there in the literature, in the Birch mechanism we have two species each in energy minima but with different electronic distributions or states. There must presumably be a transition state representing the energy high point for the electron transfer? Has anyone located such transition states or might they indeed simply be conical intersection in the energy manifolds?
I agree that different communities are not aware of the works done in their neighboring community. However, I should mention something here. I several times have heard criticisms about AIM and one of the most frequent ones is that AIM suggests presence of “non-physical” entities such as NNAs. I wonder why free electrons, loosely bonded to molecules, i.e., NNAs, are called non-physical. In particular when an old idea can go to JACS with a new name.
Sorry for sounding too grumpy in this comment.
There is a lot more to Hoffmann’s article than just the concept of interstitial quasi-atoms, and of course the name of the game is not just discovering a new concept but exploiting it.
I was at the 50th birthday bash of the Cambridge structure database last week, where I encountered 2-3 crystallographers mulling over Bijvoet’s 1951 use of anomalous dispersion to settle the absolute configuration of tartaric acid. Of course, they said, physicists knew about anomalous dispersion decades earlier, and yet they never get any credit for it! But on its own it is not useful and Bijvoet managed to do something really useful with it! To my mind, its Kirkwood working around the same time as Bijvoet, but using an entirely different technique to achieve the same result that gets perhaps less credit than he deserves.
Re non-physical manifestations of Bader’s QTAIM, the one I have heard most often is the non-physical “bond critical point” manifested in cis-but-2-ene between two hydrogen atoms. It is non-physical in a chemical sense, since the chemistry community does not find the concept of such a bond between two hydrogen atoms useful in being exploitable for them. A physicist, who is less worried about bonds, and perhaps more interested in the electron density itself, would find it entirely physical. It is in many ways a cultural thing, depending on whether the community finds it a useful concept for its own purposes.
Regarding the meaning of (3,-1) CPs (BCP or LCP) there is a general misunderstanding that is caused by Bader’s terminology. As far as I know, (3,-1) CPs are not chemical bonds for a simple reason. These CPs appear/disappear upon molecular vibrations; see for example DOI:10.1002/chem.201402177
This was not unknown to Bader either. He several times repeated that so-called “bond paths” are not chemical bonds. Finally, he wrote this paper to clarify the situation: 10.1021/jp906341r
Bader however has shown that (3, -1) CPs in electron density have a mirror image in Virial field. This can be interpreted as a local stabilization to prevent a “more severe increase” in energy of a molecule. (It may sounds weird but it is not. This is very similar to the concept of aromatic TS for concerted reactions. Nevertheless, formation of a (3,-1)CP in a strained molecule is not necessarily synonym to formation of a chemical bond. Besides, in his terminology a “bonded atomic pair” are those that are connected by a CP. This terminology is misleading but he realized that quite late. An alternative way for calling atoms, which are connected by CPs, is the term “neighboring atoms” see: DOI: 10.1002/chem.201402177.
Similarly, one can call bond critical points, line critical point (LCP) in analogy with ring and cage critical points. These are some suggestions that does not harm the main body of theory but make them less troublesome.
Thanks for that interesting insight. I am happy with the term line critical point to replace bond critical point. Of course in the vast number of cases, a LCP point will also describe a bond.
It’s my honour to hear that you liked it 🙂
I am sure replacing BCP with LCP or “bonded/nonbonded atoms” with “neighboring/non-neighboring atoms” will reduce the confusion regarding AIM. Most of critiques of AIM are just discussing about terminology. Very recently, I myself made the same mistake, did not explain terminology of my work and got a very nice paper nicely rejected! 😀
Cina,
A valuable insight from your identification of NNAs using AIM2000 was that the density is near the threshold for cutoff. One way of exploring that is to change the characteristics of the metal. ROGDAS is a lithium electride, similar to GAVKIS, but with rather smaller ligands. Some of the analogous surfaces obtained for the Li system are shown below:
NCI

MEP:

SOMO (red) superimposed upon Spin density (blue):

SOMO on its own:

The archive is doi: 10.5281/zenodo.19966.
I would be interested if AIM2000 shows NNAs for this system as well.
Well, I checked this case too but AIM2000 finds no NNA. I assume relatively considerable density of SOMO on carbons accommodates the free electron to some degrees. Then the remaining density of the free electron that should form the NNA got masked by the higher density of atoms around the NNA. I recently found a certain case in which topological features of a part of a molecule is totally masked by the electron density of the rest of atoms. That case was also an open-shell system like this. If you would like to know more, send me a private message since the paper of this certain case is not yet published. I could in that case find the missing CPs by analysing just alpha-electron density. Here also it is doable but is a bit tricky and takes some time.
P.S. My father named me after Avicenna (Ibn-Sina) “سینا in Persian”.
https://en.wikipedia.org/wiki/Avicenna
In English this name can be written both as Sina and Cina but I picked the second form 🙂 I visited China and like it but I am not China 🙂
The nominal Mulliken spin density on the Li is 1.121267, but as an atom-centered reduction this does not reveal either the radial distribution or the anisotropy of the distribution shown in the diagram above.
As for China, that is auto-correcting computers for you! I have no idea how to switch it off (must be a system thing).
I checked alpha electron density to see if I can find an NNA there. However, unfortunately, even analyzing the alpha-electron density didn’t help. Maybe the Mulliken spin density is right and the unpaired electron is accommodated so close to the Li that is indistinguishable from the rest of the electron density of the system. On the other hand, the electron can be very delocalized therefore, has no recognizable maximum in the molecular e-density. I have a question/suggestion out of my curiosity. I know it is not easy to model implicit solvents (you need many parameters to do so) but if you model the solvent medium by an implicit solvent model, the electron may emerge. Nevertheless, implicit solvent models impose an electric field to the system. A loosely bonded electron can detach in such conditions.
A GAVFIS continuum solvent model for water (an extreme case) is archived at 10.14469/ch/191346. Of course normally the molecule is embedded in a cavity excavated from the continuum dielectric field, and this cavity is evaluated for a regular Connolly surface based on standard van der Waals radii. However, what the appropriate size of the cavity for an electride should be is entirely unknown.
The various surfaces computed above certainly do respond quite significantly. For example, the SOMO energy is -0.033 au, compared to -0.056 in the gas phase. It is still bound, but much less so! Do please try to see how the NNA features respond.
I analyzed the new wavefunction. As I expected the NNA has grown up in size. I say that concerning the distances between LCPs (BCPs) that are connecting the NNAs to their neighboring atoms. I am checking the molecule by AIMAll to see if it is now distinguishable by the program.
Would you mind if I ask you let me have wavefunction of ROGDAS in a solvent. I am curious to see if the NNA appears in the solvent.
Please find the molecular graph of GAVKIS in gas-phase and solvent here:
https://www.academia.edu/13810211/GAVFIS
P.S. Feel free to edit my comment by adding the molecular graphs. The figure on fist page is the gas-phase molecular graph and the figure on the second page is that of the solvent phase.
P.S.2. Sometimes it takes some time till “Academia” allows a pdf on its pages. If you received this message “This document is currently being converted. Please check back in a few minutes.” select download pdf from top right of the page.
DataDOI: 10.5281/zenodo.20038 for ROGDAS in a water continuum field.
Cina, I am a MultiWFN user, albeit a pretty raw beginner at it. I also don’t have a lot of computation capacity at hand… but I would be glad though to give a shot at analyzing GAVKIS and/or ROGDAS.
If I’m looking at the data correctly, I believe I should download for analysis:
GAVKIS: the WFN file at citation [4] of the original post
ROGDAS: the WFN file at the DOI link at the end of Dr. Rzepa’s post at July 12, 2015 at 4:56 pm
Do you concur?
I analyzed ROGDAS in solvent but here I could not find an NNA either. However, looking at the Laplacian of the electron density confirms that where you see the SOMO lobe there is an electron concentration. This electron concentration region is not dense enough to form an individual basin. So, I scanned the Laplacian of electron density along the -z axis and found the electron concentration, i.e., negative laplacian. I must say that in solvent the electron density of the SOMO seems denser so electron concentration is more considerable compared to gas-phase. Please see the figures and plot of the Laplacian here:
https://www.academia.edu/13810211/GAVFIS
Also, as to the QTAIM nomenclatural question, the series of names concludes logically, albeit a bit redundantly, in “point critical point” for the (3,-3) CPs. In short, the CP marking an n-dimensional ‘object’ has character (3, 2n-3).
Brian,
Yes indeed, get the wf files from there. AIMALL also accepts FCHK files, but I do not know if MultiWFN does?
For anyone who has read the comments this far, but who may be unfamiliar with the QTAIM terminology used, I thought it might be useful to summarise (and if my explanation needs correction, I am sure my colleagues can provide clarifications!)
QTAIM looks at the topology (curvatures) of the electron density in a molecule. This curvature at any point in space is obtained from the second derivative of the electron density ρ(r) with respect to the three dimensions of cartesian space, a 3,3 density Hessian matrix.
The matrix is constructed only for regions of the density where the first derivatives of the density with respect to each of the three cartesian coordinates are zero, and these are known as critical points in the density.
This 3,3 matrix at critical points has three eigenvalues, and the signature of this matrix is the sum of these eigenvalues. There are four possible conditions for any given matrix:
♥ All three eigenvalues are -ve, designated (3,-3) and these are the so-called attractors. Most of the time the coordinates of this critical point coincide with a nucleus, and so these are the so-called nuclear attractors. Sometimes, the point does not coincide and these are the non-nuclear attractors or NNAs that we are discussing above. They can also be called the point critical point as Brian says above, or PCP.
♠ Two eigenvalues are -ve, one is +ve, designated (3,-1) and these are the bond critical points, or as we discuss above, better termed the line critical point (LCP) since they tend to lie close to (if the bond is bent) or on the line connecting two point critical points (if the bond is straight).
♣ One -ve and two +ve eigenvalues give rise to a (3,+1) or ring critical point or RCP.
♦ Three +ve eigenvalues (3,+3) are called a cage critical point or CCP.
The Poincare-Hopf rule states that PCP – LCP + RCP – CCP =1. Any QTAIM analysis must satisfy this condition, but that does not mean it is a complete analysis, because if for example a LCP and a RCP are in close proximity, they can annihilate and self-destruct. When this happens, the Poincare-Hopf rule is still satisfied, but two critical points have vanished!
The Laplacian of the electron density at any point, ∇2ρ(r) is the sum of the diagonal elements of the density Hessian. This sum can be -ve or +ve, and taken together with the value of ρ(r) can be used to characterise the type of bond that may or may not be associated with an LCP (previously BCP):
♠ Covalent, ∇2ρ(r) negative, ρ(r) large (> 0.2, smaller values are i.e. hydrogen bonds)
♠ Ionic, ρ(r) small
♠ Charge shift, ∇2ρ(r) positive, ρ(r) large (> 0.2)
The above really relates to the value of ∇2ρ(r) between two identical atom types (say carbon). If the atoms are different the interpretation at a single critical point is more problematic, and hence one would look at the isosurface of this function in space to draw sounder conclusions. You can inspect some Laplacian isosurfaces here.
Can I introduce you to EBEWOX, which is the exact Rb analogue to GAVFIS. The wave function is archived at doi: 56z.

Spin density:
Curiously, there is no equivalent sodium electride reported as a crystal structure.
I just want to add one point to your last comment. A better descriptor of covalency within the context of QTAIM is the delocalization index, δ(A, B). DI can be understood the best in the following format:
δ(A, B) = –2[(nAnB) – (nA) (nB)]
Here A and B are a pair of atoms, (nA/B) represents the “average population of atoms A or B and (nAnB) is the average population of an atomic pair”. Accordingly, δ(A, B) represents the number of electrons that are delocalized between a pair but do not belong to either of these atoms. This is an elegant representation of covalency, which simply recovers the concept of the “bond order”.
This factor is a more reliable index of bonding compared to LCP (BCP) since δ(A, B) works everywhere, whether LCP is present or absent between an atomic pair.
For more information also citation to LCP please see this paper: doi: 10.1002/chem.201402177.
Meeting EBEWOX was a pleasure to me 🙂 I analyzed its wavefunction and found five NNA arranged around Rb atom in a way reminiscent of sp3d hybrid orbitals. I would like to call this NNA, an sp3d NNA, if you don’t disagree. Proximity of NNAs obtained from AIM analysis to the Rb atom explains why they remained concealed in crystallography. I expect molecular motions mix the NNAs density and that of the Rb atomic center so in general no electride is expected to be distinguishable. Even if molecular motions do not affect NNAs, finding them near a large attractor should not be that easy.
Please find the molecular graph here beside the rest of systems I checked:
https://www.academia.edu/13810211/Non-Nuclear_Attractors_and_Electrides
Sorry, I think the EBEWOX file may have mislead. I forgot to mention that Rb was calculated with a pseudopotential, and I should have produced a .wfx file instead of a .wfn file. I know that AIMALL treats the density at the boundary of the pseudopotential correctly, and removes the artefacts you observed, but only if you give it a .wfx file and NOT a .wfn file.
I suspect however that AIM2000 cannot handle a .wfx file (which is relatively new)? Nor MultiWFN? The correct wfx file can be found at DOI: 10.14469/ch/191371.
I also changed basis set from 6-31+G(d) to Def2-SVP for Rb. The former includes diffuse + functions, which may not be mapped in the Def2-SVP basis. I will test this by doing a difference isosurface plot of the spin density, to see where and by how much the change in basis set influences things.
The difference spin density plot is isosurfaced at 4e-5 and represents the difference (at the same geometry) between EBEWOX calculated at the Def2-SVP and Def2-SVPP basis sets (the latter adds three diffuse functions to eg Rb). I should say this level of difference density is relatively low. The density above is contoured at 1.5e-4, so the difference spin density is about 25% of the actual spin density.
This does show that the basis set may itself have an impact upon whether NNAs are located or not.
The .wfx file for the Def2-SVPD calculation for EBEWOX is at doi: 10.14469/ch/191372.
Then I should say that AIM2000 is incapable of performing a flawless full topological analysis. WFX format as you mentioned is new and originally developed for use in AIMAll (I assume). Those NNAs around the Rb are then just artifacts due to the absence of the core electrons. However, AIM2000 can perform topological analysis on the rest of the electron density of the system. Meanwhile, I did not find any NNA by AIM2000 for EBEWOX. I am not sure if AIMAll can spot any NNA either.
MultiWFN can use WFX as far as I know but I never used it (unfortunately).
Curious about the missing analogous sodium electride — perhaps there’s a geometric/steric problem for Na+?
MultiWFN reads the .fchk, .wfn, and .wfx files just fine. It detects the ECP of the EBEWOX .wfx without difficulty and appears to process it as usual. I’m still figuring out the best way to generate results figures and post them for inspection; will do so as soon as I can. Briefly, though, MultiWFN concurs that GAVFIS has three NNAs outside the cryptand, whereas ROGDAS and EBEWOX do not.
One thing jumps out about EBEWOX — the basis set makes a huge difference in the detected CPs. MultiWFN identifies some (3,+1) RCPs *outside* the cryptand for the def2-SVP basis, whereas they are absent with the def2-SVPD basis. I assume this is just some sort of numerical artifact in the former case..?
Brian,
When dealing with diffuse electrons I suspect the quality of the diffuse functions might be critical. Simply increasing the overall quality of the basis i.e. Def-SVP, Def2-SVPD, Def2-TZVP, Def2-TZVPP, Def2-TZVPPD etc, will rapidly make the calculation unfeasible. One almost suspects the need to create a size-consistent special basis where the diffuse functions are given prominence. Perhaps such a basis exists? I get my basis sets from https://bse.pnl.gov/bse/portal, but there is nothing obvious about how to increase the quality of the diffuse functions without increasing the overall size too much? Modern balanced basis sets are improved as a whole, rather than adding add-hoc additional functions such as +, or ++ as used to happen with the Pople basis sets.
I am currently running a Def2-TZVPD calculation to see if it behaves similarly to Def2-SVPD or not.
Re missing sodium electride. The Li electride was reported with a specially designed smaller cryptand. Perhaps the same is needed for Na, i.e. a smaller cryptand than used for K and Rb. This would require special synthesis, and may simply have been too much work simply to “fill in the gap”. Or it might have been made, but failed to crystallise appropriately; I gather making and crystallising electrides is really challenging!
ORCA recently implemented the ‘minimally augmented’ def2 bases of Zheng, Xu & Truhlar (doi: 10.1007/s00214-010-0846-z), which add selected extra diffuse functions to certain elements. These bases appear not to be on BSE, unfortunately, though some ‘maug’ varieties of the cc-VxZ &c family are, which may be similarly constructed.
IIRC the extra diffuse functions were not numerous — is the software package you’re using (Gaussian?) amenable to addition of basis functions? I checked their page listing of implemented bases (http://www.gaussian.com/g_tech/g_ur/m_basis_sets.htm); the ‘ma-def2’ are not listed.
I have my images assembled from MultiWFN’s processing of the .wfn/.wfx files from all three electrides, and just need to annotate them with my comments before posting.
I’m running now an all-electron, nonrelativistic EBEWOX ORCA single-point at PBE/ma-def2-SVP; I have some hope it will complete by morning, US EDT, at which point I plan to follow with a relativistic run.
Which ECP/ECPs did you use in your EBEWOX computations? I think I can run with the ECP as well, but with ma-def2-SVP valence basis, to compare results.
What output formats from ORCA would be most useful for sharing? I can generate .wfn, .mkl, and .molden files, but I suspect they may not adhere strictly to the ‘canonical’ composition of those formats.
To complement your ORCA calculation Brian, I have repeated the Li, K and Rb electrides at the same consistent level of theory using the Def2-TZVPD basis and the PBE DFT method and the same optimised geometries as used for the previous calculations (to facilitate visualisation of difference densities). The ECP for Rb is the one defined for this basis at the Basis set exchange.
ROGDAS: 10.14469/ch/191373 (Li)
K>Na in GAVFIS: 10.14469/ch/191376 (Na)
GAVFIS: 10.14469/ch/191375 (K)
EBEWOX: 10.14469/ch/191374 (Rb)
The relativistic effect for the latter in particular will be interesting
Re Truhlar bases; one can download these directly from his group’s site and easily inject them into Gaussian. There is a ma-TZVP basis there, which may or may not yield similar results to Def2-TZVPD. Unfortunately, when one goes to the site, only Li and Cs are available (not Na, K, Rb!).
Re sharing outputs. One might presume that .wfn would be reasonably canonical, and the format most relevant here. If AIMALL cannot read it, we will alert you.
In terms of where to place the shared files, can I suggest investigating zenodo.org, which is run by CERN as a spin-out of the vast amounts of data generated by the LHC. You can assign a doi to the dataset, along with metadata which makes it more discoverable and comes with the prospect of longevity.
This seems to be emerging as a more optimal solution for researchers than the commercial file sharing sites such as dropbox or box.
I am following your comments and found one of them a bit questionable. You can run a relativistic ab initio/DFT optimization but you cannot analyze relativistic wavefunction by QTAIM. By relativistic I mean two-component and four-component relativistic not just scalar rel. Unfortunately, it is customary to analyze relativistic “electron density” nowadays but please bear in mind that QTAIM is not all about topological analysis.
Wavefunction of 2c- and 4c-relativistic computations produces spinors and for analyzing them one must perform QTAIM analysis on “current density” not “electron density”. As far as I know such theory is not fully developed yet. Even, if such theory develops, there is no guarantee that “atoms”, the most fundamental element of AIM theory, emerges from the current density analysis. Relativistic wavefunction can be a dead-end for QTAIM.
To clarify more I should draw your attention to this fact that outcome of a normal QTAIM computation, besides CPs, is atomic charge and energy. Sum of all atomic energies must be equal to the energy of the DFT/ab initio wavefunction. In case of a 2c- or 4c-relativistic wavefunction the energy obtained from “electron density” cannot be and is not equal to the energy of the wavefunction. Accordingly, a key element of the AIM that is atom is totally lost.
Cina, thank you for noting this and elucidating! I will skip the runs with relativistic corrections. Comparisons with the ECP calculations will have to suffice. Do the ECP DFT results not suffer from the same problems? That is, does ‘confining’ the relativistic effects to the ECP region(? electrons?) negate the problems with using QTAIM on the non-relativistic ‘outer’ wavefunction/density?
I will export first to wfn, see how that goes.
I cannot browse to zenedo.org; my ISP cannot resolve the DNS name. Is that the correct site?
Brain, by using an ECP you are just considering the scalar-relativistic correction, i.e., increasing the mass of electrons when they move in high-speeds near the nucleus. Outcome of an scalar-relativistic calculation is still convertible to the electron density. So, no problem. But, once you employ a 2c- or 4c-relativistic hamiltonian, wavefunction should be presented in terms of current density not electron density. Then, as I mentioned before, atoms of AIM do not appear upon topological analysis of the current density (I am just speculating; no one did it before).
There is still a possibility to convert 2c- even 4c-wavefunction to electron density. In fact, some argue that the electron density is an observable that is even experimentally measurable by x-ray crystallography for any kind of atoms including heavy atoms. However, the energy of system is not measurable from the electron density alone. That’s why we need a relativistic-QTAIM theory to work with 2c- or 4c-wavefunctions and recover not only the topological properties but also the energy of the system.
Cina, Thanks (again) for the masterclass in QTAIM.
Brian, https://zenodo.org is currently resolving here. I typed zenedo by mistake.
Most interesting. It re-raises the question, though: all of ORCA’s relativistic methods I believe are scalar-relativistic, with DKH2 and ZORA being most often used. Would either of those work suitably with QTAIM? I have never seen reference to current density in any of the DKH2 or ZORA computations I’ve run.
Cina,
Re “recover not only the topological properties but also the energy of the system.”
Is that not also an issue with other methods such as coupled cluster or CASSCF? The density is correct, but not the inferred energy?
It’s my pleasure to discuss on these issues. I am not really good at AIM but I know about these issues since I was engaged with such problems for a long time. About the problem of AIM with CC or CAS wavefunctions I should say that the problem is not inherent like the case of relativity. Some software packages do not fully support CAS/CC wavefunctions but it can be resolved.
Even non-Born-Oppenheimer AIM is recently developed for treating nuclei as wave rather than a classical particle. You can check papers of Shant Shahbazian regarding these issue.
Here is his webpage:
https://sbu-ir.academia.edu/shantshahbazian
The electrides we have thus far discussed are formed from endohedral coordination within macrocyclic ligands, which evict the single electron at least partially into a region exo to the ligand.
This morning, I attended a symposium in honour of the 30th anniversary of the discovery of fullerene, C60 given in honour of Sir Harry Kroto. Fullerene is well known to absorb up to six electrons, and unsurprisingly it forms complexes with the alkali metals:
QEJPAX: Rb4.C60, doi:10.5517/CCVD5HW
FULLER: Cs6.C60, doi:10.1038/351462a0
WESYEY: Na2.Cs.C60, doi: 10.1126/science.263.5149.950
However, all these alkali atoms (as cations) are exohedral, ie outside the cavity. It would be fun if someone succeeded in putting one or more alkali atoms inside the cavity, ie endohedral. The spin density would then reside inside or outside the cavity? Just a thought experiment!
Unpleasant discovery: ORCA’s wfn conversion only works for restricted wavefunctions. 🙁 I will be able to export to Molden format and analyze in MultiWFN, but I don’t know if the resulting files will work with AimAll / AIM2000. I will post anyways.
Thank you for the Zenodo recommendation — it looks quite suitable. I got the GAVFIS data (.wfn from citation [4] of the original post) written up and published: http://dx.doi.org/10.5281/zenodo.20376. MultiWFN indeed finds the three NNAs outside the cryptand.
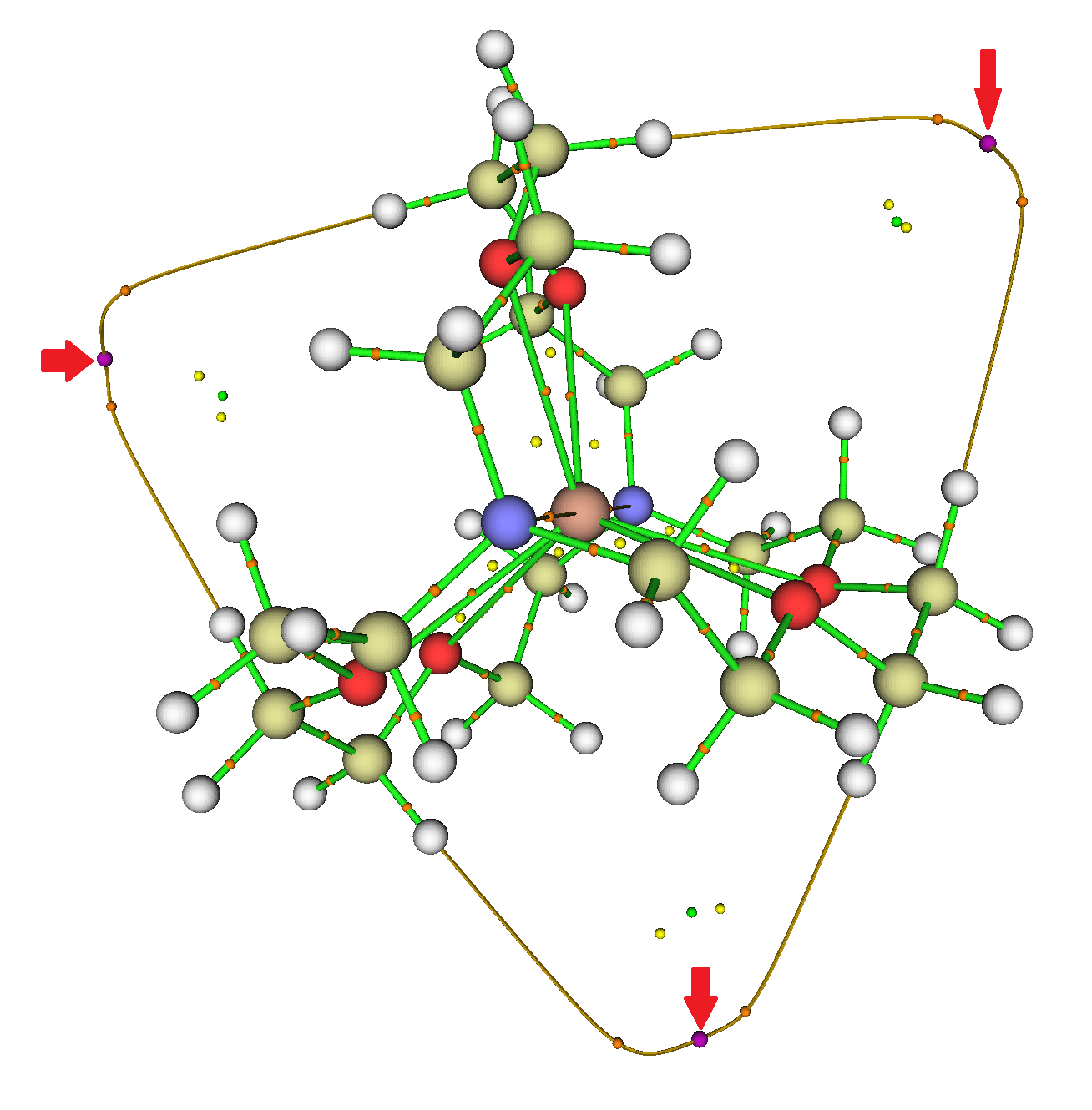 ‡
‡
In addition to the line paths between PCPs and LCPs, MultiWFN also searches for line paths between RCPs and CCPs. Interestingly, some of the latter type are found in GAVFIS, but not in a symmetry matching that of the overall system. Presumably this is either a numerical artifact… or perhaps the crystal packing distorts the symmetry?
ROGDAS and EBEWOX to follow soon…
‡Editor’s note. Diagram added from the archive cited above. For full explanation and also the other two diagrams, please visit the cited archive.
Re symmetry: GAVFIS has an interesting story to tell in this regard.
1. The crystal coordinates as retrieved do NOT have C3 symmetry, but obviously so because the coordinates of one hydrogen atom are simply missing from the CSD (crystal structure database).
2. To generate the correct structure I had to add the missing hydrogen by hand.
3. This resulted in coordinates that almost had C3 symmetry, and were not far from the even higher D3 symmetry.
4. On the assumption that my addition of that hydrogen was the cause of the desymmetrisation, I simply re-symmetrised the coordinates to C3 and optimised the structure.
5. Inspecting the orbitals produced after this optimisation of the geometry using the 6-31+G(d) basis, the top three α MOs have( E) (E) (E) symmetry. In other words the single electron is in a degenerate orbital and hence will suffer a Jahn-Teller distortion.
6. The output file for the calculation to generate the .wfn file as originally reported at doi: 10.14469/ch/191354 states “This structure is nearly, but not quite of a higher symmetry.” which suggests the symmetry is indeed broken, presumably by that Jahn-Teller effect, hence leading to the result reported in the previous comment.
7. Repeating at the Def2-TZVPD basis set level (doi: 10.14469/ch/191375) the symmetries of the top five occupied α orbitals are (E) (E) (A) (A) (A) which now suggests that no Jahn-Teller effect will operate.
So we see here a system which is on the very edge of exhibiting a Jahn-Teller desymmetrisation, depending on the nature of the basis set used.
Interestingly, EBEWOX, which is the Rb analogue, has lower C2 symmetry, but the coordinates are again not far from having D3 symmetry. So is EBEWOX slightly Jahn-Teller distorted?
In reality the spectrum of symmetries seen here are probably all covered by the dynamic Jahn-Teller effect, which is that very low barriers separate the two-possible Jahn-Teller distorted geometries and hence experimentally one would see only the average structure in eg a crystal. By coincidence, I was recently discussing the dynamic Jahn-Teller effect in the crystal structure of Cu(H2O)6 which is a d9 spin doublet.
So these topological features seem rather fragile, both to the basis set used to calculate the density and no doubt also when the vibrations are included in the picture..
Brain, Can you compute localization and delocalization indices for the NNAs by MultiWFN? Unfortunately, since AIMAll failed we have no data regarding the nature of interactions between NNAs and the rest of atoms in the system. AIM2000 can compute DI/LI but it takes ages! Literally ages! If MultiWFN can compute DI and LI in a reasonable time it would be fantastic! Then I have to start using MultiWFN 🙂
Cina,
MultiWFN is able to compute DI and LI for GAVFIS, though as with AIM2000 the calculation is quite expensive for a grid dense enough to give high quality results. There are four default grids; it crashes my computer if I try to use the top two (“High” and “Lunatic”), though, there is a settings change that might fix this. The cheapest grid (“Low”) is relatively quick (a few minutes), but the software warns of poor accuracy. I’m rerunning on the “Medium” grid now, which looks like it will take about 20-30 minutes to generate the grid and then 3+ hours to calculate the overlap matrices.
Unfortunately, the output is poorly conditioned for quick analysis. In particular, I’ve not found a good way to match the basin attractors to the atoms except by importing to Excel and checking distances. Not a challenging analysis, but most of my time was spent just reformatting the data more usefully. If I were going to do this often, I would be writing a script for it, for sure.
I’ve pulled together the “Low” grid data (arbitrary NNA indexing; DDIME = diagonal DI matrix element):
NNA1 — LI: 0.003, DDIME: 0.108
NNA2 — LI: 0.003, DDIME: 0.109
NNA3 — LI: 0.003, DDIME: 0.099
All of the other attractors have DDIME greater than one, except for the central potassium:
K — LI: 16.156, DDIME: 0.492
I’m not very familiar with LI & DI — if DDIME is not the relevant quantity, please advise. Also, I can post my Excel sheet for further analysis, if desired.
Ahhhh.. rereading the (de)localization section of doi:10.1007/s10698-012-9153-1 (Bader & Matta, 2013), what I should have reported for K was 16.156/19 = 85%. Also, the DDIME is just the sum of all of the nondiagonal elements of the corresponding row (or column) of the DI matrix — if that’s helpful.
Broadly, averaged over all atoms of the same type, if I’m calculating/interpreting correctly:
K: 85% localized
O: 96% ”
N: 83% ”
C: 63% ”
H: 41% ”
s.d.’s for O’s and C’s are about 3 percentage points; those for N and H are about 1 percentage point.
Brain,
I am uncomfortable with your %LI values.
LI for oxygen seems odd to me. Oxygen has two covalent bonds with its neighboring carbons. From its population that cannot br greater than 9.5 at least 1.5 electrons must be shared. So, %LI most be roughly around 80%. A percent localization of 96% suggests a totally ionic bond. I have seen such %LI for example for atoms in NaCl. Also 85% for K seems huge. K is so electropositive and most be positively charged with very small delocalization. Even if K shares one electron from its 19 electrons with the rest of the system, which is unexpected, its %LI cannot be less than 90%. I am skeptic about the outcome of MultiWFN.
BTW, could you find any NNA for the other systems by MultiWFN?
Cina,
Your argument makes good sense to me — I’m not sure what I can say, though, these are the numbers it’s giving, and I know very little about the theory (viz., the form of the Fermi hole function) or the implementation.
The results from the “Medium” grid computation are different, but not dramatically, and it still sees the O electrons as having very high LI:
K: 90.5% localized
O: 96.4% ”
N: 86.7% ”
C: 61.5% ”
H: 41.8% ”
Is it possible this is some sort of unusual situation, the system being an electride? Say, the potassium is inducing extreme localization on the oxygens, while the carbons and hydrogens bear the delocalized electron?
In any event, the overlap computation happily ended up taking only about an hour, instead of 3+ hours like I’d estimated.
—
I do not see any NNAs for ROGDAS or EBEWOX.
MultiWFN finds one each extra RCP and CCP for ROGDAS (image at http://dx.doi.org/10.5281/zenodo.20554); no idea what, if anything, this means.
EBEWOX has some H—H LCPs at the periphery of the system, connected by line paths, that I also found interesting. I found a measure of diffuse-function dependence of the found CPs for EBEWOX in my own computations, also. (EBEWOX data still pending analysis and deposition to archive.)
(Dr. Rzepa, is it possible for us as commenters to embed the images directly in comments, via an <img> tag or somesuch, or can only you do that?)
Dear Brian, it seems that increasing the grid at least improved the situation for K but oxygen seems still weird. It is very unlikely to me to have an oxygen with such a high localization index. As I mentioned that suggests that oxygen has very little covalency. I guess you have a large error in the charge and energy of your system.
I checked my computations on GAVFIS by AIMAll. Although, it does not find the NNAs, it still shows a reasonable LI/DI. I see %LI for atoms like this:
Atom %LI
K 98.64
O 86.68
N 77.41
C ~64
H ~41
These values make sense since they are in line with the usual number of electrons each system has in its valence shell.
It seems that we are still far from a perfect AIM software 😀
AIMAll failed to recognize the NNA and AIM2000 and MultiWFN are so slow and unreliable for integration.
Cina,
I ran a PBE/def2-SVP computation of the GAVFIS monocation — no electride, just the cationic complex — and the LI values ended up much the same as for the electride proper. Either there’s something unusual about the complex more broadly, or MultiWFN is not doing a good job at the LI/DI calculation.
Can you suggest a good model system on which I can test the LI/DI calculation, to confirm the problem lies with the software? Benzene? Anthracene?
Cina,
For a sanity check, I ran MultiWFN on methane and water using the ‘lunatic grid’:
H2O (lunatic grid):
************ Total delocalization index matrix ************
1 2 3
1 1.39238548 0.69617672 0.69620876
2 0.69617672 0.70484081 0.00866409
3 0.69620876 0.00866409 0.70487284
Total localization index:
1: 8.431 2: 0.084 3: 0.084
CH4 (lunatic grid):
************ Total delocalization index matrix ************
1 2 3 4 5
1 3.92664883 0.98166050 0.98166067 0.98166088 0.98166677
2 0.98166050 1.11566808 0.04466893 0.04466899 0.04466966
3 0.98166067 0.04466893 1.11566841 0.04466913 0.04466968
4 0.98166088 0.04466899 0.04466913 1.11566873 0.04466973
5 0.98166677 0.04466966 0.04466968 0.04466973 1.11567584
Total localization index:
1: 3.845 2: 0.490 3: 0.490 4: 0.490 5: 0.490
CH4 is one of the systems reported in Bader & Matta (2012), and the carbon LI of 3.845 / 6 = 0.64 and hydrogen LIs of 0.49 match the values in Table 2 relatively well (0.661 and 0.469, respectively). The C-H DI values also match well; 0.982 here and 0.980 in Bader & Matta.
Water behaves more strangely — the LI is *greater than unity* (1.054), implying (if I understand correctly) a significant charge transfer from the hydrogens to the oxygen, charge which is then apparently being held localized in the oxygen basin. This notion of significant charge transfer is supported by the integrated electron density in the basins:
O: 9.128 e-
H: 0.436 e- (both atoms)
Total: 9.9998 = 10.000 e-
Intuitively, I agree with you: the electrons in the oxygen basins should *not* be so strongly localized, with the atoms being covalently bonded to neighboring carbons.
What if they are so strongly localized? Oxygen is second only to fluorine in electronegativity, and in Bader & Matta they have calculated LIs for a number of perfluorinated molecules (LiF, BeF2, BF3, CF4, NF3, and SiF4). In all but one case (93.2% for NF3) the LI of fluorine is 95% or above. On an intuitive level, I would consider fluorine covalently bound to carbon in CF4. But:
LI[C] = 0.705
LI[F] = 0.950
DI[C-F] = 0.441 (much less than unity, implying a significant mix of covalent and ionic character)
[By the way: Dr. Rzepa, thank you for permitting us this extended exploration in your comment thread–it’s been tremendously educational and enjoyable.]
Re “is it possible for us as commenters to embed the images directly in comments, via an![]() tag or somesuch, or can only you do that?)”
tag or somesuch, or can only you do that?)”
The inability for commentators to embed images is apparently a deep rooted design feature of the WordPress software, and is done in the interests of “security”. You might not be aware that a vast number of attempts to post comments by spammers occur on a daily basis, all fortunately trapped by the Akismet software used on the blog. I think it was felt that the consequences of even one of these getting through onto the blog and containing an image would be far too serious to allow. It might also be that if a image can be uploaded to the blog, it might in fact turn out to be a virus or Trojan, and wreak havoc. Whereas the text only that can currently be entered into a comment cannot contain destructive components.
I will continue to retrieve images from remote locations and edit them into comments as appropriate or of course on request.
Also apologies to Cina. The WP blog remembers some but not apparently all previous commentators and allows their posts to appear automatically. For reasons that still baffle me, Cina’s posts continue to require manual authorisation by myself, and so may sometimes take a few hours, as was the case this morning.
Re “[By the way: Dr. Rzepa, thank you for permitting us this extended exploration in your comment thread–it’s been tremendously educational and enjoyable.]”
As Cina pointed out in an early comment, there is considerable myth, and often misunderstanding about aspects of QTAIM, often reduced/trivialised to “the physicists vs the chemists”. I have found these discussions truly helpful in dispelling at least some of these myths, and am very happy and grateful that you have chosen to participate in this way!
Dear Brain,
I think I understood what is the problem with your %LI values. If I am wrong please correct me. You are computing %LI by dividing LI on the atomic number of atoms, e.g., ” LI of 3.845 / 6 = 0.64 “.
The “percent localization” as defined by Bader is the “average population” of an atom over the “total population”. Let me explain what is what 😉
The electrons are dynamic and their population in an atom is not constant in fact. So, if you measure the number of electrons in an atomic basin by time, you see it is fluctuating through time! The average population of an atom or localization index is the number of electrons that reside inside an atomic basin, i.e., never leave the basin, or it’s better to say, it is the minimum population of an atom. Total population of an atom is sum of the minimum population (LI) plus half of the DI, i.e., those electrons that are shared between an atom and its near and far neighbors. Total population defines atomic charge; atomic number minus total population gives you the charge of an atom. For defining the %LI you should divide LI on the total population not atomic number. Once you do it, the mystery of your %LI values will solve 🙂
I am right now writing a manuscript on the concept of bond order and hope I can push it for publication into a journal that people care about it. All these issues are discussed there in a simple language. Wish me luck please!
Dear Prof. Rzepa,
no problem about comments 🙂 The only thing makes me laugh is that every time I press submit comment button, I have to confirm I am a human.
I am really happy that you provided this opportunity to discuss about these issue. These discussions are really useful for me too as I learn which parts of theory are not well-known yet and I can emphasis on them more in my works.
Just to tidy up one variable. I have run GAVFIS using the larger Def2-TZVPD basis set. The three NNAs found by Cina and now Brian are still there.
And I can conform there are no NNAs for the sodium analogue of GAVFIS or the Rb EBEWOX at Def2-TZVPD.
I forgot to respond to one question from Brain. About CF4, which is indeed a controversial case, I should say it is a covalently bonded system. Then, if it is covalent, why DI is so low between C and F and chare of C and F are so big. The answer is indeed simple within the context of chemistry. C-F bond is a polar covalent bond. A polar covalent bond is of course a bond that benefits from both electron sharing and charge-shift. Please note that charge-shift or charge transfer has a different meaning in NBO for example. In some theories charge-transfer means covalency, i.e. electron transfer from a filled to an unfilled orbital. However, when we talk about charge shift in AIM we simply mean inequality of charge distribution, i.e., ionicity. Therefore, C-F bond is covalence but its bond order is less than one because charge shift has reduced the covalent bond order and made the bond a polar-covalent bond. In order to gauge bond order it is highly recommended to compare DI for a new species with the DI of a known species with widely accepted bond order. Then if we say C-F in CF4 has bond order of one, we can compare other C-F bonds in other compounds by measuring the increase/decrease of DI and relating it to the bond order. Right now an example came to my mind. What is the bond order of C-F bond in fluorobenzene? How efficient is the back bonding from p-orbitals of F to pi* of benzene? As I remember from my BSc organic chemistry, reactivity of fluorobenzene is comparable with benzene while it has a highly electron withdrawing F as a substituent. I remember it was rationalized by back-donation from F to benzene.
Maybe the answer of this question is already known. Prof. Rzepa knows much more about chemistry than me. But, if it is not known yet, one can study it by comparing the DI of C-F in CF4 and that of fluorobenzenes.
In the post, I included an ELF basin analysis of GAVFIS. The location of the two additional basins, close to the nitrogen atoms seemed odd and out of congruence with the other analyses. I had previously used the Topmod09 program for such analysis.
I then noticed that MultiWFN also supports ELF analysis (and much much else), and that it naturally runs in parallel (TopMod09 does not). So I gave GAVFIS a go, using the more recent and accurate Def2-TZVPD wavefunction and starting with a much finer grid than was feasible with Topmod09. The result is shown below, and it nicely replicates the three fold symmetry of the other functions. The basin integration is 0.154 each, of 0.45 in total. This allows us to state that about half of the upaired electron is in the diffuse “interstitial” space surrounding the molecule, and the rest resides on or within the molecule itself.

I have to say I am very impressed with multiWFN so far! A new toy to play with!
Indeed – even one such image slipping through would be a most unpleasant occurrence. A wise policy.
Ever since I started reading about QTAIM a few months ago, I’ve found it odd that it hasn’t been more accepted, even if not embraced, by the quantum chemistry community. After all, the underpinning principle of DFT (coarsely paraphrased, at least) is that ‘everything is in the density.’ Bader’s QTAIM, too, explicitly founds itself on analysis of the properties of the density–by what argument would one accept the former but not the latter? A great pity if it really has just been unfortunate nomenclatural choices leading to the conflict.
Cina, I am tremendously relieved that the LI discrepancies are from my error and not a problem with MultiWFN! Your description makes perfect sense: LI = |F(A)| / N(A), *NOT* |F(A)| / Z_A as I had been doing. From scratch, using the cheapest grid MultiWFN took about 15-20 minutes on three cores to generate basin populations and LI/DI information, with following data workup requiring 10 minutes or so. Resulting %LI for GAVFIS:
H: 41.8%
C: 65.7%
N: 75.4%
O: 86.5%
K: 96.6%
NNA: 5.4%
Much better!
I have two final observations to make from my computations on EBEWOX, dealing with inclusion of extra diffuse functions. Once I get my Zenodo upload structure for full computation datasets figured out, I will present them here.
I’m glad that I was able to introduce a new toy! I’m most appreciative to the development group in China for making it available. Also, Dr. Rzepa, on a personal note: one of the things that keeps me coming back to your blog is the obvious fun you have while noodling at chemistry. I really enjoyed your posts on your chemical explorations in your youth — the SO2-whitened grass and purple-smoked garden path were especially memorable.
Here are ELF analyses for EBEWOX (Rb), Na and ROGDAS (Li).
Rb:

This one is very similar to K albeit with a smaller interstitial electron occupancy of 0.36e.
Na:

shows some difference, having only two ELF basins in the interstitial regions, these integrating to 0.62e. This might be a case for reducing the size of the grid spacings to see if this difference is simply an integration error.
Li

This again shows three ELF basins, integrating to 0.62e.
So, ELF shows interstitial electron basins for Li-Rb, whereas QTAIM shows only NNAs for K.
Note added. For the Na electrode (not derived from a crystal structure), improving the integration grid by halving the interval size yields the same result of only two ELF basins. It is worth noting that apart from the integration, one also obtains the volume of the basin. For the two basins, the volumes are ~13,000 a.u.3. The other basins range from 1 to 3500 a.u.3, which illustrates the diffuse nature of the electride anion.
I have just returned from a two day meeting celebrating the 30th birthday of C60. Sir Harry Kroto gave the plenary naturally, and having fun was the very point that he made repeatedly in his talk. He regretted that since young chemists nowadays have to focus on the impacts of everything they do, perhaps some of the fun has now gone out of it!
C60 was identified spectroscopically in 1985, and made in pure bulk form in 1990. Ever since then, a steady stream of people ask what use is it? Even Harry felt he had to put up at least one slide showing how it might be useful.
Re EBEWOX: it would appear that adding extra diffuse functions to the basis can influence the found CPs. Computing EBEWOX at PBE/SVPall for Rb and PBE/def2-SVP for all other elements, the following CPs are found (dataset w/image):
The red arrows indicate ring CPs and cage CPs on the periphery of the system that vanish upon adding a single additional diffuse function to Rb using the “minimal augmentation” approach of Zheng et al.: (dataset w/image):
Adding further diffuse functions to Rb or to the remainder of the system does not noticeably change the CPs found, though the effect on the calculated energy is significant:
Baseline: E = -4205.174906 Eh
+1 on Rb: dE = -1.06 kcal/mol
+2 on Rb: dE = -1.21 kcal/mol
+3 on Rb: dE = -1.24 kcal/mol
+1 on all but H: dE = 25.65 kcal/mol
I would assume the significant benefit gained from adding diffuse functions on all heavy atoms derives from the sheer number of additional functions added, as well as the non-spherically-symmetric nature of the delocalization of the electron.
(Note: MultiWFN reads the Molden files of the datasets just fine, but other software not configured to handle data generated from ORCA may fail.)
Brian, I am happy to see you solved the problem. I was so amazed by those numbers at first. I think I have to start using MultiWFN too!
Prof. Rzepa,
I appreciate physics community for one reason. They do not care about application as much as chemists. Instead physicists enjoy the sheer joy of understanding more often than us.
Brian wrote “. After all, the underpinning principle of DFT (coarsely paraphrased, at least) is that ‘everything is in the density.’”
To that I would add that the density is a direct observable, and that QTAIM on measured densities is occasionally performed (e.g. 10.1002/anie.200500169)
It is a mystery to me why more such studies are not done. Put simply, X-ray crystallography normally only measures density around a nucleus (i.e. a PCP) but rarely at a LCP. Of course, one needs a synchrotron to do so, but there are plenty of these in national laboratories.
Here is a fascinating report of a new type of electride, Na2He, in which helium, if not exactly conventionally bonded, is an essential molecular component of the system. DOI: 10.1038/nchem.2716 with a commentary at gizmodo.com/a-wild-new-helium-compound-could-rewrite-chemistry-text-1792042165.